Concurso
Primero, lee las reglas del juego. Después, responde a los problemas.
FÁCIL:
En un reino muy lejano (no especifica si en el tiempo o el espacio, pero creo que no es importante) un rey decidió solventar una disputa entre dos caballeros de una manera, desde su punto de vista, muy ingeniosa e innovadora. Les propuso que hicieran una carrera de caballos y el ganador de la misma sería entonces quien tuviera razón. Pero lo ingenioso era que ganaría aquel cuyo caballo llegara último a la meta. Los caballeros montaron y …. no se movieron. Durante horas permanecieron inmóviles en sus briosos corceles. La contienda empezaba a ser un poco aburrida, con aspecto de poder llegar a durar varios meses, o años, o incluso, varias generaciones, cuando un sabio profesor de matemáticas, que estaba entre el público, se acercó a los jinetes, les susurró algo al oido y finalmente hubo un vencedor.
¿Qué fue lo que el sabio profesor de matemáticas dijo a los caballeros?
27-11-2007 por Viasil
|
|
MEDIO:
| Con los números 4, 5 y 6, utilizándolos una sola vez, conseguir el 27.
4-11-2007 por Fidias
|
|
DIFÍCIL:
16 personas deben resolver un problema en una serie de reuniones.
Para ello cada una las personas debe haber trabajado con las otras alguna vez, pero no pueden trabajar las 16 juntas. Cuando dos reuniones no tienen participantes en común se pueden realizar simultáneamente (es decir, el mismo día). Dos personas que trabajaron juntas una vez ya no pueden volver a hacerlo.
El objetivo es llevar a cabo el cometido en el menor número de días posibles.Una posibilidad: el primer día podrían trabajar 15 personas juntas, y en los 15 días sucesivos cada una de estas 15 personas trabajar con la que quedo fuera el primer día. Se necesitarían entonces 16 días.Otra posibilidad: se forman 2 grupos (A y B) de 8 personas cada uno: a1,…a8, el primero y b1,…,b8 el segundo. El primer día trabajan el grupo A y el B paralelamente. El segundo día a1 con b1, a2 con b2 hasta a8 con b8. El tercer día a1 con b2, a2 con b3 hasta a8 con b1. Se sigue así hasta el último día que se juntan a1 con b8, a2 con b1, a3 con b2 hasta a8 con b7. Se necesitan entonces 9 días.1. ¿Es esta la cantidad de días óptima o se puede hacer en menos días?
2. ¿En cuántos y cómo?
17-10-2007 por Viasil
|
|
RANKING:
|
4053…………………….. 27 puntos
Fernando…………….. 15 puntos
Viasil…………………….. 12 puntos
Jordiel………………….. 10 puntos
Fidias……………………….5 puntos |
El juego consiste en resolver los problemas planteados. Hay 3 niveles de dificultad (Fácil, Medio y Difícil). No es necesario responder a los 3 a la vez, basta con resolver uno de ellos. La persona que resuelva un problema tiene derecho a plantear uno nuevo, manteniendo el nivel de dificultad, de modo que siempre haya un problema de cada tipo sin resolver. Si dos días después de resolver bien un problema el acertante no ha planteado uno nuevo, perderá ese derecho y cualquier otro concursante podrá hacerlo. No se puede plantear un nuevo problema sin que se haya resuelto el que esté planteado en ese momento.
En el caso de que algún problema se resista, se pueden dar y pedir «pistas». No se debe abusar de las pistas, es decir, no está bien pedir una pista el mismo día que se plantea un problema. Primero hay que «darle al coco».
Se puntuarán las soluciones correctas de la siguiente forma:
PROBLEMA FÁCIL………. 1 Punto
PROBLEMA MEDIO…….. 3 Puntos
PROBLEMA DIFÍCIL….. 10 Puntos
Los puntos se irán acumulando hasta el final del juego. Actualmente se está jugando la EDICIÓN 1, que concluirá cuando un participante alcance los 100 puntos. En ese momento comenzará la siguiente Edición. Al inicio de cada Edición, todos los participantes tienen 0 puntos.
El ganador de cada Edición, además del honor de ser el vencedor y del sabor de la victoria, recibirá un premio material.
Se aceptan todo tipo de sugerencias, que podéis hacerme llegar a través de los comentarios o en un mail a concursoNSM(arroba)gmail.com
Estos fueron los primeros problemas:
FÁCIL:
Calcula:
82.315 x 12 x 3’29 x π x 5.321.428 x 0 x 27’19 x 54 = ¿?
MEDIO:
Calcula:
(x-a)·(x-b)·(x-c)·(x-d)·………·(x-y)·(x-z) = ¿?
DIFÍCIL:
Halla el siguiente número:
720, 504, 336, 210, ¿?
en el problema fácil es 0
en el problema difícil es 142
FACIL: =0 (dado que se multiplica por 0)
MEDIO: =0 (existe el término (x-x)=0)
DIFÍCIL: = 120 (ya que 336=6*7*8, 210=5*6*7 y 120=4*5*6…)
¡¡Muy bien!! Te estrenas con un triplete. Ya tienes 14 puntos.
Te toca poner un problema de cada tipo. Haznos pensar, 🙂
Raül, estamos esperando por los nuevos problemas. Si estás por ahí, deja un comentario con los enunciados o envíamelos al mail, para que el concurso no esté mucho tiempo parado. Si no puedes o no quieres, dímelo y pongo yo unos nuevos.
Saludos.
Raül debe estar de vacaciones, porque no responde.
Para que el juego no se detenga, propongo nuevos problemas:
FÁCIL:
¿Cuál es el único número que tiene tantas letras como indica su cifra?
MEDIO:
Una persona camina a 2 km/h al subir una cuesta, y a 6 km/h al bajarla. ¿Cuál es la velocidad media para todo el recorrido?
DIFÍCIL:
Halla el siguiente número:
83.473, 130.283, 194.453, 279.823, ¿?
He actualizado el post principal con los nuevos problemas.
la del medilo la velocidad promedio es 3km/h
Lo primero y lo segundo lo tengo, pero el tercero no lo veo por más que pruebo. Y como no quiero facilitar la cosa, sigo probando lo tercero 🙂
No hace falta responder a los tres, Juanjo. Es más, por lo que me han dicho, el tercero es bastante difícil, aunque aún no sé si creérmelo. En parte lo he puesto para despejar dudas sobre su dificultad.
Vete pensando problemas nuevos y responde cuando quieras a los que quieras.
Un saludo.
1. Cinco
2. 4 km/h
Lo tercero no lo veo ni de broma por más que he probado…pero no me rindo 🙂
Al igual que Juanjo, el 3º no me sale. Seguiremos intentándolo.
Un saludo
Juanjo, respuesta correcta a la primera pregunta, pero siento decirte que el Nivel Medio te ha engañado. Debo recordaros que, más que de matemáticas, son problemas de «pensar» (aunque hay matemáticas, claro).
4 km/h es la solución rápida, pero equivocada 🙂 Tienes que darle una vuelta más (al coco).
Cuando quieras puedes proponer un problema sencillo, que actualizo el post.
Creo que entonces la solución al de nivel medio es 3 km/h…
Uno que leí por ahí, fácil:
Imagínate que pilotas un avión de pasajeros en medio de una tormenta. Un relámpago cae sobre el motor de la derecha y lo destroza, viendo que con un solo motor no se podrá llegar al próximo aeropuerto se decide tirar por la puerta toda la carga. Después de vaciar medio avión solo queda el pasaje, compuesto por un equipo de jugadores de fútbol, veinte monjas claustrales, un grupo de turistas japoneses y varios ejecutivos de una multinacional petrolífera y Kim Bassinger. ¿Como se llama el piloto?
Jajaja, muy bueno, Juanjo. Lo he puesto ya en el post principal.
En cuando al segundo, la respuesta es correcta aunque te voy a pedir lo mismo que a mis alumnos, pero antes te voy a contar un chiste:
Entra nuestro protagonista a un manicomio y, para pasar el rato, decide hacerles preguntas a los internos. Le pregunta a uno:
– Oye, ¿cuánto da 3 por 2?
El loco responde:
– Mil.
«Vaya como está el personal» piensa nuestro protagonista, y le hace la pregunta a otro:
– ¿Cuánto da 3 por 2?
– Febrero – responde el loco.
«Vaya, este está aún peor, voy a probar con el siguiente»
– ¿Cuánto da 3 por 2?
– Seis – dice el tercer loco.
Extrañado por la respuesta correcta, nuestro protagonista, continúa:
– Tú no estás tan loco como los demás. ¿Cómo los has sabido?
Y el loco responde:
– Fácil, he dividido Febrero entre mil.
Entenderás a qué viene el chiste y qué es lo que les pido a mis alumnos: explica un poco tu respuesta 😛
Ah, y vete pensando un nuevo enunciado para el nivel medio.
Saludos.
Jajajaja, bonito chiste…y más aún con febrero, el mes «menos divisible» 🙂
Me explico:
Tarda el triple en subir que en bajar…luego habrá que considerar la velocidad de subida tres veces más que la de bajada para obtener la media:
(2km/h x 3 ) + 6km/h =12
Todo dividido entre 4, para valorar el triple la velocidad de subida…
Resultado: 3 km/h
Espero que sea esta la explicación…creo que es lógica.
Mi prueba de nivel medio, un silogismo.
Deducir la conclusión a partir de estas premisas:
1. Un queso suizo tiene agujeros.
2. Cuanto más queso, más agujeros.
3. Un agujero ocupa el espacio que ocuparía el queso.
4. Cuantos más agujeros, menos queso.
Saludos.
Ahora sí, Juanjo. Para los que no entiendan la media ponderada, lo explico con un ejemplo sencillo:
Si la cuesta tiene 6 km, en subirla (a 2Km/h) tarda 3 horas y en bajarla (a 6km/h) tarda 1 hora. Tiempo total: 4 horas.
Espacio total: 12 Km (6 de subida y 6 de bajada)
Velocidad Media: Espacio/Tiempo = 12km/4h = 3km/h
En cuanto a tu propuesta, me arriesgo a responder, aunque creo que me he liado:
Las proposiciones 1 y 3 son información. Las que tienen implicaciones son la 2 y la 4. A más queso, más agujeros, y a más agujeros, menos queso. Si las unimos, obtenemos la proposición 5: a más queso, menos queso.
Por otra parte, podríamos poner las inversas de la 2 y la 4: A menos queso, menos agujeros, y a menos agujeros, más queso, con lo que obtenemos la proposición 6: a menos queso, más queso.
Uniendo las proposiciones 5 y 6 (a más queso, menos queso, y a menos queso, más queso) obtenemos un bucle del que no sé salir o un estado de equilibrio en el que el queso ni aumenta ni disminuye.
En cualquier caso (bucle o equilibrio) no sé continuar y, lo peor de todo, es que no sé a dónde hay que llegar.
Seguiré intentándolo.
Apunte: este silogismo podría servir como ejemplo para la función seno (o coseno): un sube-y-baja que se prolonga hasta el infinito.
joe que difíciles, no valgo para esto da-beat 😦
Jaja, Davich, no son tan difíciles. Los que tú pusiste en el Team eran más complicados. Todavía recuerdo las vueltas que le di al del camión y el pájaro… y lo sencillo que era al final.
La respuesta al nivel fácil es: Yo xD, ya que el mismo enunciado dice que lo piloto.
Ahí va otro para el nivel fácil:
c,u,d,t,c,¿?
Diría que da-beat ha clavado la solución al de nivel medio… la primera parte, porque lo de las inversas ya es para nota, y no creo que sea tan complicado.
El de nivel difícil aún no lo he sacado :(.
Pues he encontrado una solución lógica al problema del queso. Si unimos la proposición 4 (cuantos más agujeros, menos queso) y la inversa de la 2 (cuanto menos queso, menos agujeros) obtenemos la proposición: cuantos más agujeros, menos agujeros, que tiene cierta lógica ya que, cuanto más agujereado esté el queso, menor número de agujeros hay, ya que son más grandes. El caso límite sería en el que no hay queso, que esta totalmente agujereado (más agujeros), y solo tiene un agujero (menos agujeros).
Caul, creo que tu respuesta al nivel fácil es correcta, así que pongo tu nuevo enunciado en el post principal, aunque esperamos la confirmación de Juanjo.
Saludos.
Muy interesante este blog.
Me ha gustado lo de la lejanía de los objetos 😉
da-beat eres nusero verdad? y ese cambio de nick 😛 ??
Venga tío un saludo, pasaré cuando pueda por aquí 🙂
Jaja, hola Davich, bienvenido. Deberías haber respondido a la pregunta del nivel fácil de Caulfield.
Lo de los nicks es debido a que, de tanto multiplicar, multipliqué mis personalidades 😛
Pásate cuando quieras, te esperamos.
Perdón por la demora, estaba de viaje. La repuesta al que puse de nivel fácil depende de quién sea el interrogado…evidentemente si eres el piloto, la respuesta es tu nombre. El problema gana dicho…porque al leerlo se puede volver sobre el inicio, pero al oirlo se pierde la nota inicial entre tanta información inútil.
Por lo que respecta al del queso, no solo es correcto Da-beat, sino que amplias las posibilidades. Inicialmente pensé en la solución «Cuanto más queso, menos queso», pero es válida la variante que propones.
Pienso los nuevos…
Jajaja, y yo seguía dándole vueltas. Siempre me ha pasado lo mismo con la lógica, que no sé a dónde hay que llegar ni dónde hay que parar.
Después pongo uno de nivel medio, entonces.
Bueno, aquí va mi problema del nivel medio:
Si S(1997)=1-2+3-4+5-6….+1997 y S(1998)=1-2+3-4+5-6….-1998, ¿cuánto vale S(1997) + S(1998)?
Ya está actualizado en el post principal, arriba.
Intentaré el de nivel medio 🙂 :
Por lo que parece,
S(1) = 1
S(2) = 1 – 2 = -1
S(3) = 1 – 2 + 3 = 2
S(4) = 1 – 2 + 3 – 4 = -2
S(5) = 1 – 2 + 3 – 4 + 5 = 3
S(6) = 1 – 2 + 3 – 4 + 5 – 6 = -3
…
Es decir, para N=número natural y S(N)=número entero:
S(N)= -N/2, si N par
N/2+1, si N impar
Por lo tanto, S(1997) + S(1998) = (1997/2+1) + (-1998/2) = 999 – 999 = 0
Espero no haberme liado xD.
Lo haya hecho bien o no, propongo otro de nivel medio para que lo tengas en la recámara 🙂 :
Si a, b y c son variables binarias (pueden valer 0 o 1), y las operaciones (+,*,’) equivalen a las funciones booleanas (OR,AND,NOT) respectivamente, ¿cuál es el resultado más simplificado de esta expresión?
b*[a*c*(a+c*a’)]+[ [a*(b+a)]*(a+c)’ ] = ¿?
Muy bien, Caulfield, aunque creo que tienes un «piccolo errore»: para N impar no es N/2+1, sino (N+1)/2. Solo es de notación, porque los cálculos están correctos.
Aún así, había una manera más sencilla, agrupando términos:
S(1997)=(1)+(-2+3)+(-4+5)+….+(-1996+1997)
S(1998)=(1-2)+(3-4)+(5-6)+….+(1997-1998)
Cada paréntesis en el primer caso vale 1 y en el segundo -1. Es fácil ver que hay el mismo número de paréntesis en cada caso, con lo que la suma de los dos da 0.
Tienes tus tres puntos y he actualizado el post con tu problema. Voy a estudiar funciones booleanas y lo pienso.
Aaaah, ok, yo lo que hacía era realizar la división entera (truncando el decimal) en lugar de la real, pero como apuntas es más correcto.
Y tu método es más elegante, cómo no, el mío es más ingenieril xD.
Fácil: U
Medio: a·b·c
Difícil: 390233
Si son correctos decídmelo y demuestro como he llegado al resultado y pongo tres problemas nuevos muy interesantes. Si no lo son avisadme y seguiré intentándolo.
Jordiel, el difícil (que lo planteé yo) no es correcto, pero has estado muy cerca. Sí me gustaría saber cómo has llegado a ese resultado. Normalmente en este tipo de problemas, si pones la solución con el razonamiento, no hay muchas dudas en el caso de ser correcto. Ya te digo: andas muy cerca. Ánimo, que lo consigues.
En cuanto a los de Caulfield, los debe confirmar él, pero creo que el fácil es incorrecto y el segundo correcto. Espero que aciertes, porque ya me ha entrado curiosidad por esos «tres problemas nuevos muy interesantes».
Saludos.
Como bien sospecha da-beat, la solución al de nivel medio es correcta, pero la del fácil no… lo que nos da a entender que da-beat se está conteniendo para no barrernos a todos, jajaja xD.
Jordiel, veo porqué dices que la respuesta es «U»… de hecho podría ser una solución de la serie, tal vez tendría que haberla hecho más larga para eliminar otras opciones. Si queréis digo la letra que sigue y que la incógnita sea la siguiente, seguramente estará más claro.
Saludos.
Llevo desde las 16:30 intentando resolver los problemas y no hay manera.
El valor 390233 lo he sacado haciendo diferencias entre los números contiguos,
luego volviendo a hacer lo mismo con los resultados y la última diferencia la con-
sidero constante.O así creía yo que era.
Me conectaré más tarde para seguir dándole al coco
Jajaja, Caulfield, no es exactamente eso. Las bases del juego están pensadas para que, al proponer vosotros problemas, pudiera pensarlos yo también, pero no con la idea de participar activamente. Quiero que juguéis vosotros, pero si solo proponía problemas yo, para mi iba a ser aburrido. Así, yo también me divierto, pero sin jugar (aunque de vez en cuando no pueda evitarlo y responda 🙂 ) Salvo esas excepciones, yo solo soy el moderador del juego.
En cuanto al fácil, es buena idea poner una o dos letras más. Es fácil cuando sabes la solución, pero reconozco que me costó un poco sacarla y creo que a los demás le pasa lo mismo, porque nadie más ha respondido. Posiblemente hubiera sido más fácil si no hubieras puesto la primera C, por la costumbre, ya sabes 😛
Jordiel, sí, con tu razonamiento sale 390233, pero el problema es suponer que la última diferencia es constante cuando ninguna de las anteriores lo había sido. Simplemente lo haces porque no tienes más diferencias, pero no tienes base para hacer esa suposición. Si hubiera dado 5 números en vez de 4, habrías supuesto la diferencia constante en el siguiente paso.
A lo mejor me pasé de difícil, pero ya os dije que en parte era un experimento para despejar dudas sobre su dificultad. Aún tengo esperanzas en que alguien lo saque. Deciros que las diferencias no es el camino. Y, por si alguien le estaba dando vueltas, el siguiente número NO acaba en 3, ese tampoco es el camino.
Ánimo y recordad: 10 puntos son 10 puntos, no iban a ser regalados 😛
jaja, pues si algo tenía más o menos claro del de nivel difícil era que acaba en 3 xD. Y también probé lo de las diferencias, pero veo que tendré que tomar otro camino.
Bueno, pues ahí van dos letras más para el de nivel fácil; con las otras queda:
C,U,D,T,C,C,S,¿?
La «facilidad» de este problema está precisamente en que sabemos que es fácil, y por lo tanto la respuesta es un poco tonta, el enfoque es diferente al de otros problemas de series.
Caulfield, al releer mi anterior comentario, me he visto a mi mismo como a Blaine el Mono, buscando adivinanzas. Quizá esa sea otra de mis personalidades 😛
Jordiel, cuando quieras puedes plantear uno para el nivel medio. Ya te he sumado los puntos y actualizado la serie de Caulfield. Seguro que ahora te resulta más fácil.
Problema de nivel medio:
Un hombre paseaba por la calle cuando de repente encontró una moneda de 1€. El individuo, muy contento, siguió caminando y de nuevo, se cruzó con otro botín. Ésta vez fueron 2€. «Hoy es mi día de suerte» pensó mientras caminaba y, aún no había salido de su asombro cuando aparecieron 3€. Siempre que caminaba encontraba un botín 1€ superior al anterior hasta que encontró una última cantidad, 2546€.
¿Cuánto dinero ha recaudado el hombre?
Intentar demostrar «geométricamente» (creo que se dice así) la solución
Muchas gracias, Jordiel, por tu enunciado, ya está en el post principal.
Ahora todos a pensar y hacer cuentas 🙂 a ver quién se lleva los 3 puntos.
Ya he vuelto de vacaciones…
FACIL: S (de S-iete, O-cho…)
MEDIO: Forzando un poco lo de «geométrica» diría que usando los números triangulares tendríamos que calcular el 2546-ésimo número triangular, es decir = 3242331 $$ T_n=\frac{n (n+1)}{2}$$
DIFICIL: pensando…
NUEVAS PROPUESTAS:
FACIL: Queremos cortar un pastel de forma cilíndrica en 8 partes iguales, pero solo usando 3 cortes. ¿Cómo lo haremos?
MEDIO: Encontrar un número de 4 cifras autoreferente de la siguiente manera: El primer dígito indica el número de ceros que forma el número total, el segundo dígito indica el número de unos, y así el número de doses y el de los treses para las siguientes.
Es correcto Raül, perdóname si no he expresado bien el enunciado. No había caído en el problema Fácil, y en el Díficil sigo pensando todavía.
Raül, te toca formular dos nuevos problemas.
Bueno, Raül, otra vez aquí y arrasando. Muy bien. Con tu permiso, voy a rebajar un poco el nivel en la respuesta al Medio, que viendo la tuya igual hay gente que se asusta:
Si encontramos 1€, luego 2€, etc, lo que tenemos es una progresión aritmética, en la que cada término es 1€ mayor que el anterior, empezando por 1. Si queremos saber cuánto dinero ha recaudado el hombre después de haber encontrado 2546€, tendríamos que sumar 2546€ a todo el dinero que ya había encontrado, esto es, 1+2+3+4+…+2545. En total tenemos la suma de todos los números enteros desde el 1 hasta el 2546.
Viene de perlas la anécdota de Gauss, según la cual, el profesor, para mantener callados a sus alumnos durante un rato, les propuso sumar todos los números desde el 1 hasta el 100. El jovencito Gauss le dio la respuesta en un momento: 5050. El profesor quedó sorprendido y le pregunto cómo había sumado tan rápido. Nuestro amigo Gauss lo único que había hecho era darse cuenta de que el primero más el último (esto es 1 y 100) sumaban 101, lo mismo que el segundo y el penúltimo (2 y 99), el tercero y el antepenúltimo (3 y 98), etc. Haciendo parejas de este tipo, tenemos 50 parejas que suman 101, con lo que la suma será 50·101=5050.
En nuestro caso tenemos que sumar desde 1 hasta 2546. Vemos que las parejas 1 y 2546, 2 y 2545, 3 y 2544, 4 y 2543, etc suman siempre 2547. Tenemos 2546/2=1273 parejas, luego el resultado de la suma será: 1273·2547, que da 3242331, como bien dijo Raül.
La solución geométrica consiste en dibujar un triángulo de puntos, en el que arriba haya 1 punto, en la siguiente fila 2 puntos, en la siguiente 3, etc. De este modo, un triángulo de una fila tendría un solo punto, un triángulo de dos filas tendría 1+2=3 puntos. Uno de 3 filas, 1+2+3=6 puntos. Es por eso que a los números 1, 3, 6, 10, 15, etc se les llama «números triangulares». Hay una fórmula para hallar estos números, que es n·(n+1)/2, donde n es el número de filas del triángulo. Así, un triángulo de 6 filas tendrá 6·7/2=21 puntos. Si dibujamos un triángulo así formado por 2546 filas, el total de puntos del triángulo sería 2546·2547/2, que sería el caso de nuestro problema.
Ha quedado un poco más largo, pero espero que también un poco más claro. Ya he puesto tus enunciados en el post principal. Muchas gracias por tu colaboración, Raül.
Perfecto, Da-beat. También conocía la historia de Gauss, es un monstruo.
Respecto a mi problema, sólo quería que tuvierais en mente que la fórmula n·(n+1)/2 se puede interpretar como la mitad de un rectángulo de lados n y (n+1) para luego, más adelante, cuando tenga oportunidad de poner otro problema, poder debatir entre todos otra cuestión más que, bajo mi punto de vista, es muy interesante.
Creo que tengo las soluciones de los 2 primeros problemas, pero el Difícil se resiste. Si averiguo éste último pondré las soluciones de todos.
Pues ya estamos esperando esa cuestión, y si tiene debate, mucho mejor. (Oye, os funciona eso de ponernos los dientes largos, al menos conmigo)
Ah, y no es necesario responder a los tres en el mismo post, como habrás podido comprobar. Si tienes soluciones, ponlas, que se te pueden adelantar.
Saludos y ánimo con el Difícil, que ya sale.
Soluciones:
FÁCIL: Creo que se consigue cortando dos veces por la mitad formando una cruz, luego amontonamos las 4 partes que nos quedan una encima de otra y hacemos un último corte nuevamente por la mitad obteniendo 8 partes iguales.
MEDIO: 1210. El primer dígito (1) indica un cero, el segundo (2) indica dos unos, el tercero (1) indica un dos, y el cuarto (0) indica que no hay treses.
DIFÍCIL: Imposible. Como no deis pistas…
Si son correctas avisadme y pongo dos nuevas.
Jordiel: La respuesta de la fácil no era la que yo tenía en mente, de hecho podría hacerse sin manipular tanto el pobre pastel. La del nivel medio es correcta.
Pues corto el pastel en cruz y luego por la mitad de su altura. Yo creo que es correcto, así que ahí van unos nuevos.
Problemas:
FÁCIL: Seis toreros en una plaza redonda (1111110), se reparten (/) entre todos tres toros (3). ¿Qué dice la gente?
MEDIO: ¿Cuánto es el resultado de la suma 1+4+9+16+25+36+•••+(2546)»? ¿Cuál sería la fórmula para la enésima suma? Intentar darle una interpretación geométrica a esta fórmula.
Aclaraciones:
FÁCIL: los seis unos se refieren a los toreros, el cero a la plaza redonda y el símbolo (/) al de fracción.
MEDIO: el símbolo («) significa el exponente cuadrado.
Jordiel. ya están puestos los enunciados en el post, así como tus puntos. Para los demás: tened cuidado, que Jordiel y Raül se están distanciando 🙂 y subiendo el nivel, el sumatorio de los cuadrados no sé si entra en el nivel Medio. El próximo ha de ser más sencillo, o menos matemático, que si no nos olvidamos el «nosolo» que precede al «mates», ¿ok?
Discúlpame da-beat, pero no mientras que para ti estos problemas están chupados. Resuélvelo y te planteo una cuestión (esta cuestión no entra en el concurso, sólo es una curiosidad) para conocer tu opinión al respecto.
Jordiel, la intención del blog en general y del concurso en particular, es que sea accesible para cualquier persona a partir de, aproximadamente, 2º o 3º de E.S.O. (14-15 años). Obviamente, algunos contenidos requieren conocimientos de bachillerato, pero intento que sean los menos posibles. A lo largo de todo el blog he utilizado simetrías, figuras planas, sistemas de coordenadas, series y progresiones, multiplicaciones, porcentajes, estadística básica (percentiles, diagramas)… todos ellos contenidos cursados antes de los 15 años. Solo en algún post he hablado de trigonometría o funciones exponenciales.
El concurso se sitúa dentro de ese marco, preguntas de pensar, más o menos complicadas, pero que se basen en conceptos matemáticos sencillos. Incluso el problema Difícil actual, además de ser una serie, solo utiliza (sirva esto como pista) potencias y restas. Todos los problemas planteados hasta ahora han cumplido ese requisito, excepto el de binario de Caulfield y este tuyo del sumatorio de los cuadrados. Tu anterior problema (los números triángulares) también lo cumplía, ya que era la suma de una progresión aritmética, que se cursa en 3º.
No te parezca mal, pero no quiero excluir a nadie del blog ni del concurso por culpa de contenidos de alto nivel. La dificultad de los problemas ha de estar en los razonamientos, no en las matemáticas. No tienen que ser problemas de matemáticas, esos ya se resuelven en clase. Tienen que ser problemas de «nosolomates», no sé si entendéis el concepto.
En cuanto a la cuestión de la que hablas, si es fuera de concurso, puedes hacerla cuando quieras. Lo digo porque voy a dejar el problema para que lo resuelva otro 😛
Caulfield seguro que conoce la fórmula y su interpretación geométrica y doy por supuesto que Raül también.
Saludos.
Mi cuestión es: si en mi primer problema de nivel medio la fórmula n·(n+1)/2 se puede interpretar como la mitad de una superficie rectangular de lados n y (n+1), y en este último problema de sumatorios de superficies la fórmula se puede ver como la tercera parte de un volumen (no doy más pistas), ¿en el sumatorio de los cubos la fórmula podría verse como la cuarta parte de una pieza de 4 dimensiones? ¿Qué pensáis al respecto?
Muy buena tu pregunta. Te contesto lo que se me ocurre, pero me lo pensaré más detenidamente.
La suma de los números enteros, de fórmula n·(n+1)/2 se puede interpretar como la mitad de una superficie rectangular (de un paralelogramo, en realidad) como dices, o también como el área de un triángulo (b·h/2).
La suma de los cuadrados, tú la ves como la tercera parte de un volumen (de un paralelogramo, imagino), pero puede verse también como el volumen de una pirámide. Me es inevitable responder al problema: la fórmula que pides es n·(n+1)·(2n+1)/6. En la fórmula no se aprecia ni la tercera parte de un volumen, ni el volumen de una pirámide, pero sí se hace con la interpretación geométrica: Se trataría de hacer una piramide con cubitos, en la que cada sección horizontal (cada «piso» de la pirámide) es un cuadrado. Es decir, sería una pirámide de base cuadrada. Arriba del todo hay 1 cubo, debajo, un cuadrado de lado dos (cuatro cubos). La tercera sección, un cuadrado de lado 3 (9 cubos), etc. Cada piso es un cuadrado. En el problema que planteaste, tendríamos una pirámide de 2546 pisos, en la que la planta baja es un cuadrado de lado 2546. Si sumamos los cuadrados (sumamos los pisos) tendremos la suma de todos los cubitos que componen la pirámide, es decir, su volumen.
Hasta ahí con las dimensiones «cómodas». Si hacemos un ejercicio mental como el planteado en el post «Uno de dimensiones», e imaginamos qué ocurriría si damos un nuevo salto, se me ocurre que la suma de los cubos podría ser el hipervolumen de una hiperpirámide (o como se llame el equivalente en 4D de una pirámide). De hecho, la fórmula es n^2·(n+1)^2/4. Si consideramos n como una longitud, eso se mediría en m^4 (metros a la cuarta), que sería correcto. ¿Es o no es? Eso se sabrá cuando despeguemos de nuestro mundo de 3 dimensiones y podamos «ver» las demás dimensiones. Hoy por hoy solo es un
a pajaejercicio mental.Y tú, ¿qué piensas al respecto?
Correcto da-beat. Aún te falta decir el resultado de la suma, pero con la fórmula ya es evidente.
Ahora te toca plantearnos un problema de nivel medio.
En cuanto al tema de las dimensiones, como no entra en el concurso te respondo en «Una de dimensiones» que le viene como el anillo al dedo.
Para el de nivel fácil: 1111110/3 = 370370, que visto en una calculadora, y dándole la vuelta, se lee OLEOLE.
Puntito a puntito os alcanzaré xD!! Por cierto, da-beat, en las reglas pone que el de nivel fácil vale 0 puntos, es un error, ¿no?
Para el de nivel difícil estoy por pasarlo por una red neuronal artificial, a ver qué sale, jaja, aunque hay pocas muestras.
Ahí va uno de nivel fácil:
Queremos llenar de agua un depósito y disponemos de 3 mangueras diferentes. La primera manguera tarda 30 horas en llenarlo, la segunda tarda 40 horas y la tercera tarda 5 días. Si para llenarlo lo más rápido posible utilizamos las tres a la vez, ¿cuánto tiempo tardará en llenarse?
Iremos resolviendo los sencillos, mientras me rompo la cabeza con las potencias y restas del difícil:
FÁCIL: Tarda en llenarse 15 horas, ya que cada manguera llena 1/30, 1/40 y 1/120 del depósito cada hora respectivamente.
PROPUESTA: Uno muy sencillo SIN hacer apenas cálculos:
En un torneo de tenis participan 72 jugadores, se juega por eliminatorias (si gana sigue adelante, si pierde se elimina). ¿Cuántos partidos se han disputado al final del campeonato?
Solución al problema DIFÍCIL: 390617
La serie de números del enunciado responden a la función f(n)=16(n^4)+32(n^3)+24(n^2)+18n-127. Para n=8, f(n)=83473. Para n=9, f(n)=130283. Para n=10, f(n)=194453. Y para n=11, f(n)=279823. Siguiendo la serie, para el siguiente número natural, n=12, f(n)=390617.
Gracias a la pista de da-beat he podido deducir la fórmula: lo que hice en un principio fue tomar 83473, le aplico la raíz cuadrada (288.91694…), lo redondeo (289), lo elevo al cuadrado (83521) y, por último,le resto 48 (83473). En resumen, 83473=(289)^2 -48. Si aplico el mismo proceso a los siguientes números de la serie, me sale: 130283=(361)^2 -38; 194453=(441)^2 -28; 279823=(529)^2 -18. Si nos fijamos, 361-289=72; 441-361=80; y 529-441=88. Esto por un lado. Luego tenemos los valores 48, 38, 28 y 18. Entonces, para calcular el siguiente número de la serie, sumamos 96 a 529, lo elevamos al cuadrado y le restamos 8. Quedaría así:(625)^2 -8=390617.
Problema nuevo DIFÍCIL: La Hipérbola Escondida.
Me he tomado la molestia de pasar por cada una de vuestras casas y dejaros un obsequio: ¡una hipérbola! (en la mayoría de las casas he sido más generoso y he dejado más de una. No soy Papá Noel, que conste). Es muy caprichosa, se esconde en tu casa y aparece a ciertas horas del día. Se manifiesta como hipérbola en condiciones normales pero si la encuentras, ¡podrás transformarla en otras figuras! ¿Qiuén será capaz de encontrarla primero? Decir cómo y qué formas puede adoptar.
Bueno, bueno, mientras yo he estdo de boda, veo que habéis estado «currando», y con buenos resultados, por lo que veo. Voy por partes:
Nivel Fácil: Veo que Caulfield acertó el problema de Jordiel, y ya puso un problema que respondió correctamente Raül. (Lo explico, por si acaso: Como dice Raül, una manguera llena 1/30 del depósito cada hora, otra 1/40 y otra 1/120. Entre las tres, cada hora llenan, sumando lo anterior y simplificando, 1/15 del depósito. Por lo tanto, tardarán 15 horas en llenarlo) También hay nueva propuesta. He sumado vuestros puntos (Caul, tenías razón, estaba equivocado: es 1 punto) y actualizado con el enunciado más reciente.
Nivel Medio: Lo había respondido yo y tengo pendiente un nuevo problema. Lo pondré dentro de un rato, que primero he de contestar a los otros comentarios.
Nivel Difícil: Correcto, Jordiel. Solo un detalle. Fíjate que 289 es 17^2, 361 es 19^2, 441 es 21^2 y 529 es 23^2. Así no hace falta hacer las restas para ver la relación entre los números. Era, «simplemente»: 17^4-48, 19^4-38, 21^4-28 y 23^4-18. El siguiente término será, por tanto 25^4-8, que es, como bien dices, 390617.
Te llevas los 10 puntos. También he actualizado con tu nuevo enunciado. Muchachos, ¡otra vez a pensar!
DIFICIL: La hipérbola se define como la intersección de un cono con un plano inclinado cierto ángulo respecto de la base. Entonces supongo que cuando encendemos una lampara (a ciertas horas del día) el CONO de luz intersecciona una pared (PLANO), creando una hipérbola. Si movemos la lámpara podemos crear otras curvas cambiando el ángulo, creando parábolas, elipses o circunferencias.
PROPUESTA: Situémonos en una isla pequeña de vegetación abundante, la cual está rodeada de tiburones. Si un lado de la isla comienza a arder, y el viento está a favor del fuego, ¿cómo haremos para salvarnos de ese infierno?
No se si el anterior se ajusta al grado de difícil, pero realmente cuesta buscar uno «sin pasarse»
Bueno, aquí va mi enunciado para el nivel medio:
«Hallar el número que, si se multiplica por 3, da un resultado capicúa. Si se multiplica por 6, también. Lo mismo que si se multiplica por 9, 12, 15, 18, 21, 24 y 27, siempre se obtienen números capicúas.»
Solución DIFÍCIL: morirnos e ir al cielo.
Jordiel, esa es una solución fácil a un problema difícil. Algo no cuadra.
Además, como dijo alguien una vez, rendirse no es la respuesta. 😛
Vale, pues me quedo en la orilla, o arranco todas las plantas, o cavo un agujero y me escondo… No sé 😦
Jordiel, que el fuego se acerca…
Es curioso este problema, y es difícil por lo paradójico de la solución. Los que vivimos en zonas con riesgo de incendio sabemos la solución, porque es un método utilizado en la realidad para la extinción de los mismos. Seguro que a ellos también les costó dar con la solución.
PD: Me había despistado y no había actualizado el post principal con ese enunciado. Supongo que la respuesta de Raül al problema de la hipérbola era correcta, así que tiene 10 puntos más. Ya está corregido.
Mmmm, Raül a solo un punto de ganar, y Jordiel a solo 13 y ninguno de los dos se decide a responder… parece que os da vergüenza ser el ganador.
¡Ánimo, y a rematar!
:), ando un pelin liado…
A lo unico que he llegado es a que dicho capicúa tendria que ser multiplo de 7560, la cual cosa tendria que acabar en cero y.. empezar por cero?? que capicúa mas raro. no?
No, no, Raül, el número no es capicúa, son los resultados de multiplicar ese número por 3, 6, 9… los que son todos capicúas.
Suerte.
Uff, y yo pensando que el capicúa tenia que ser el mismo!
RESPUESTA = 37
Efectivamente, Raül:
37×3= 101
37×6= 202
37×9= 303
37×12= 404
37×15= 505
37×18= 606
37×21= 707
37×24= 808
37×27= 909
Y enhorabuena!! Has llegado a los 32 puntos, con lo que te conviertes en el ganador del concurso. Voy a estudiar los errores y aciertos de esta edición, para mejorar las bases y en breve dará comienzo otro turno.
Entre las cosas buenas a destacar, lo principal es vuestra participación. Gracias, gracias, gracias. Como véis, cabía la posibilidad de terminar el 31 de diciembre en el caso de que nadie llegara a los 30 puntos. Eso era porque no estaba seguro de la participación que iba a tener, y por ello debo daros las gracias a Raül, Jordiel (casi lo consigues), Juanjo y Caulfield. A todos los que habéis seguido el concurso sin atreveros a contestar, ya habéis visto cómo es, os animo para la próxima edición, que intentaré mejorar en lo posible.
Un saludo a todos.
Enhorabuena Raül!!!Me ha gustado mucho el concurso.
Ha sido estupendo participar da-beat,y seguro que para la próxima vez volveremos a estar ahí.
Saludos cordiales 😀
Pues te esperamos. Ahora estoy conociendo a mis nuevos alumnos y compañeros. A ver si alguno se anima también a participar. Cuando tenga un rato mejoro esto y dará comienzo de nuevo. Posiblemente el fin de semana.
Saludos y enhorabuena por tu segundo puesto, que tampoco está nada mal.
Gracias a todos por las felicitaciones. Espero que en una nueva edición pueda poner problemas que se ajusten más al nivel requerido y sean mas de «pensamiento lateral».
Bueno, pues con un poco de retraso, da comienzo la EDICIÓN 1 del Concurso NoSoloMates.
He dejado el problema difícil que quedó sin resolver en la anterior edición y añadido uno Fácil:
Hoy es Miércoles. ¿Qué día de la semana será dentro de 2000 días?
y uno Medio:
El 95% de las personas que aprobaron el último examen de Matemáticas tenían más de 15 años. Si se presentaron al examen 38 personas, ¿cuántos suspendieron?
Para que tenga más emoción, el total de puntos a alcanzar para ganar el concurso será de 100, en lugar de los 30 experimentales.
Espero que la participación sea por lo menos igual a la de la Edicion 0 y, por supuesto, espero que lo paséis mucho mejor.
Y nada más: Preparados…. Listos…. ¡YA!
¡Que gran página!
FACIL: Lunes
MEDIO: 18
El problema medio es interesante. La información relevante es que el 95% de los aprobados son un número entero (salvo si era en la escuela de Jack el destripador) con lo cual como aprobados (a) y suspensos (s) suman 38 tenemos: a + s = 38
pero 95*a/100 = 19*a/20 al ser 19 primo tenemos que a puede valer múltiplos de 20, en este caso sólo vale 20 luego el número de suspensos fue 18.
NUEVO FACIL: Propongo el siguiente, tal vez demasiado fácil juzgad vosotros mismos: que letra viene en la serie siguiente: L,M,M,J,V,S, ?
NUEVO MEDIO:
Varios gorriones llegan al tejado de una casa en el que hay cierto número de antenas de televisión. Si sobre cada antena se pone un solo gorrión quedan n gorriones volando. Si sobre cada antena se posan n gorriones, quedan n antenas libres. Determinar el número de antenas que hay en el tejado de la casa.
DIFICIL: creo que quemar en el sentido del viento a unos metros detrás de nosotros de tal manera que tengamos un intervalo al cabo de un tiempo en el que esa zona esté libre.
Si esta es la solución he de decir dos cosas. 1) es el fuego el que va a merced del viento y no al revés. 2) el suelo quema demasiado tras un incendio 3) los tiburones sólo cazan al amanecer y al anochecer (jejeje)
Propongo esta adivinanza (para seguir en la misma onda) a la espera de la evaluación (XD):
Jorge le dice a Juan que su bisabuelo obtuvo al terminar la Primera Guerra mundial una condecoración por su valor. Juan incrédulo le pide pruebas a lo que Jorge responde invitándolo a ver dicha condecoración. La misma era una insignia en la que se podía leer: «Por su valor y coraje durante la Primera Guerra Mundial», Juan rápidamente comprendió que era falsa.
¿¿¿Cómo lo supo???
¡Muy bien, 4053! (Ya nos dirás el porqué de ese nick. Yo he hecho la descomposición en factores, pero no me dice nada)
El Fácil era calcular el resto de la división 2000/7, que serían los días que sobran al agrupar en semanas. Sale 5, por lo que, 5 días después de un miércoles, es un Lunes.
El Medio está bien respondido y bien explicado. El truco para resolverlo era que el 95% de los aprobados tenía que ser un número entero.
En cuanto al difícil, lo planteó Raül, pero me arriesgo a decir que esa es la respuesta correcta. Como dije, ese método se utiliza a veces en la extinción de incendios: Hacer un fuego controlado por delante del incendio en la dirección en la que avanza. De ese modo, cuando el incendio llega, ya no hay nada que quemar y actúa como cortafuegos. En cuanto a tus «dos» apuntes 😛 no entiendo el primero, si lo dices para exlicar la solución o como problema a la misma. En el segundo te doy la razón, pero creo que quemarse los pies es el «mal menor». Y del tercer apunte, darte las gracias por la información, no lo sabía (aunque personalmente no me metería en el agua con ellos aunque fueran las 4 de la tarde). Muy buena también tu nueva propuesta, le estoy dando vueltas, pero no caigo. Juan es más listo que yo.
Un saludo.
da-beat deberías mandar tu página como correo en cadena, o como mensaje subliminal a ver si alguien se anima. XD jejeje
A ver, que soy nuevo en esto…
FÁCIL: D (Lunes, Martes, Miércoles, Jueves, Viernes, Sábado y… Domingo)
MEDIO: 6 antenas.
Planteando el problema con a: antenas y g: gorriones, quedan un par de ecuaciones qure son
g=a+n para la primera afirmación, y
a=n+g/n, para la segunda (con lo que ya se impone que g ha de ser divisible por n)
Resolviendo, queda que:
a=n(n+1)/(n-1) y g=(2n^2)/n-1.
Para que g sea entero, las únicas opciones son n=2 ó n=3 (para valores superiores de n, 2n^2 ya no es divisible por n-1.
Y con ambos valores de n sale a=6.
DIFÍCIL: Es falsa, porque si se la concedieron en la PRIMERA GUERRA MUNDIAL, no podían saber que era la PRIMERA (quedaban 21 años para la segunda). Así que debería de poner algo a sí como «durante la GRAN GUERRA».
¡Un saludo!
Mira, ya se han animado, y muy bien, por lo visto.
Fernando, a primera vista todas tus soluciones son correctas. La de la I Guerra Mundial, ya me parecía que tenía que ser algún detalle como ese. (Muy buena esa pregunta, 4053) En espera de que 4053 confirme que las soluciones son correctas, vete pensando en los nuevos planteamientos, aunque hasta mañana no voy a poder ponerlos en el enunciado principal.
Un saludo.
Perfecto Fernando, y gracias por resolverlos porque estoy deseando ver nuevos problemas.
Saludos.
Bueno, pues ahí van mis propuestas:
FÁCIL: Al numerar las páginas de un libro muy grueso, el editor ha utilizado 2989 dígitos. ¿Cuántas páginas tiene el libro?
MEDIO: En el bolsillo de un pantalón nos encontramos una factura en la que se lee:
72 pollos asados _67.9_ euros,
donde el primer y el último dígito del precio se han desgastado, con lo que son ilegibles. ¿Cuáles son esos dígitos, y cuánto costaba cada pollo asado?
DIFÍCIL: En una habitación cerrada nos dicen que hay una bombilla, y fuera tres interruptores, uno de los cuales enciende la bombilla. ¿Cuál de ellos es? Podemos accionar los interruptores tanto como queramos, pero sólo nos permiten entrar una vez a la habitación para comprobar.
¡Un saludo!
Ya están tus propuestas en el post principal, así como tu puntuación. Imagino que 4053 ya estará resolviéndolos. ¡Ánimo!
Hola de nuevo.Tengo la solución del problema DIFÍCIL:
Para empezar numeremos los tres interruptores:el 1,2 y 3.Comienzo activando un interruptor (por ejemplo el 1),espero durante un tiempo y activo otro(el 2) y dejo sin activar el 3.En ese instante voy hacia la habitación de la bombilla rápidamente,y lo que me puedo encontrar es:
-que la bombilla está apagada:correspondería al interruptor Nº3,porque no la he accionado.
-que la bombilla está encendida.En este caso pruebo a acercar la mano a la bombilla:si está caliente sería el interruptor 1,porque la tengo accionada durante un tiempo;y si está fría sería la 2,porque la acabo de encender.
Nueva cuestión DIFÍCIL:
Pepe y Juan están conversando.Durante la conversación Pepe le pregunta a Juan:
-Hace tiempo que no sé nada de tus tres hijas,¿cuántos años tienen?
Juan le responde:
-El producto de las tres edades son 36,y la suma de las tres edades es el número de tu portal.
-Me falta un dato-dijo Pepe.
-¡Ah!La mayor toca el piano-concluyó Juan.
¿Cuántos años tienen cada una de las tres hijas de Juan?
Al FÁCIL podría responder que el libro tiene 1494+1 =1495 páginas pero tengo un libro ruso de física que cuenta como páginas la portada también, de manera que no está tan claro…
Para el MEDIO diría que las condiciones sobre el precio son:
– el precio total ha de ser divisible por 72.
– el precio unitario no tiene cifras más allá de la centésima.
– las cifras borradas tienen valores que van de 0 a 9
Es cuestión de recordar que la suma de las cifras de un número divisible por 3 suman otro número divisible por tres, esto y que el precio total ha de acabar en un número par. Tras esto descartamos los que tras la primera división por 2 den un número impar, (sólo necesitamos dividir 92, 94, 98 para comprobarlo), luego lo mismo pero al dividir por 3 (de nuevo tomamos 92, 94, 98), tras este proceso que bien hecho dura unos 5 minutos (o menos si nadie te ha robado la calculadora) obtenemos cuatro posibles valores: 67.92 :::: 367.92 :::: 667.92 :::: 967.92
El precio borrado es 367.92 euros y el precio por pollo asado es 5.11 euros.
NOTA: 3 + 6 + 7 + 9 + 2 = 27 jejeje.
Para el DIFICIL de Jordiel diria que 2 – 2 – 9 ya que al obtener todas las descomposiciones sólo se repite la suma de 13 en 2-2-9 y en 1-4-9 de ahí la necesidad de añadir el nuevo dato.
Aunque no hace falta, la resolución del DIFÍCIL de Jordiel es correcta, aunque diferente a la que tenía en mente, es la cosa de este concurso, ¿no, da-beat? En cualquier caso, el espíritu es el mismo. Bien también la resolución del MEDIO por parte de 4053. Pero la del FÁCIL no es correcta. Y para evitar líos con los rusos (;-p) digamos que la portada no cuenta. Sólo las páginas numeradas.
¡Un saludito!
4053,es correcta tu solución,pero tienes un pequeño error:1+4+9 no son 13! :O
Fernando,tu solución que tenías en mente seguro que también es correcta,porque como ya sabes,siempre hay varias soluciones para un mismo problema. 😀
ups! perdón, lo hice en una hoja y copie mal quería decir que el otro dato era 6-6-1 lo cual justifica como decía el porké de que el padre diga ‘la mayor toka el piano’.
Bueno Fernando en vista de que el libro no es ruso ( XD ), y de que lo interpreté mal recordando una adivinanza cuyo truco consistía en no contar las pirmeras hojas del libro (cosa que hacen algunos editores) creo que el número de páginas debería ser: 1249
Vamos a ver, que últimamente escribís más de lo que puedo atender 😛
Jordiel, en tu respuesta al problema de las bombillas, hay un «piccolo errore»: Si mantienes pulsado el interruptor 1 un rato y luego enciendes el 2, al entrar, la bombilla solo puede estar encendida si el interruptor bueno es el 2. En el caso de que fuera el 1, la bombilla estaría caliente, pero apagada. Como el truco, básicamente, estaba en la idea de «la bombilla caliente», se acepta como válida. (No sé si por eso no era la respuesta que Fernando tenía en mente).
4053 acertó la del nivel medio del precio de los pollos, creo que lo explicó bien, aunque yo hubiera dicho que, por tener que ser divisible entre 72, tiene que serlo entre 9, en vez de entre 3 (la suma de las cifras múltiplo de 9, no de 3). En ese caso uno se queda solo con la solución: 367’92.
4053 también respondió bién al de las edades de las hijas. El número del portal era el 13, que no lo decía el planteamiento, pero es el único caso que nos obliga a pedir un nuevo dato, para decidir entre 1-6-6 y 2-2-9. Como dice que la mayor toca el piano, no puede ser 1-6-6 porque hay dos mayores.
En cambio, creo que la solución al problema fácil vuelve a ser incorrecta. A ver si alguien se anima con él.
Saludos.
FACIL:
Páginas con 1 digito => 9 *1 = 9
Paginas con 2 dígitos => 90 * 2 = 180
Páginas con 3 dígitos => 900 *3 = 2700
paginas con 4 dígitos => 9000 *4 = 36000
Como solo necesitamos 2989. 9 + 180 + 2700 = 2889 dígitos las 999
primeras páginas. Y por tanto necesitamos 100 dígitos mas en páginas
de 4.
100 / 4 = 25 páginas de 4 dígitos.
999 + 25 = 1024 páginas
Desde luego es más fácil como tu dices da-beat la respuesta al MEDIO.
Por otro lado, tal vez torpemente, reitero mi respuesta al FÁCIL. Lo explico a ver si es que lo estoy entendiendo mal:
Las primeras 9 páginas usan 9 dígitos, las páginas desde 10 a 99 usan 2 cada una, por lo tanto 2*90=180, las páginas de 100 a 999 usan 3 dígitos cada una, de donde 900*3=1800, de momento tenemos ya 1989 dígitos ‘usados’, quedan pues por explicar los otros 1000 dígitos, como las páginas siguientes tendrán 4 dígitos se necesitan 250 páginas más, el total hace 1249 páginas.
Mientras escribía se me ha adelantado Fidias, demostrando además que erro en la multiplicación. jajaja. me consuela que el razonamiento estaba bien falló la capacidad de cálculo.
Efectivamente, da-beat, esa era la respuesta que tenía en mente para los interruptores, con la bombilla apagada caliente de por medio… Y por fin Fidias da con el resultado. Curioso cómo a veces nos parece lo más correcto del mundo algo como 9*300=1800, y no damos con el error…Y a veces pasa en clase, perdido en una pizarra de números… Pero es buen consuelo saber que el razonamiento era correcto, 4053 jejeje…
¡Un saludo!
Bueno, pues estamos esperando por los nuevos enunciados. 4053, tienes que proponer uno de nivel medio y otro difícil. Y Fidias, uno fácil.
He revisado las respuestas y, en el de la bombilla, yo también cometí un pequeño error, porque daba por supuesto que solo se puede encender un interruptor cada vez. Supongo que 4053 quería decir que se accionaba el 2 sin apagar el 1. En ese caso estaría bien su respuesta, la bombilla puede estar encendida y caliente o encendida y fría (o menos caliente, por lo menos)
Lo dicho, estamos con «mono» de nuevos problemas.
Yo no hablé del problema de la bombilla, los rayos catódicos nos despistan a todos XD. Como problema DIFICIL: un monje sube a las 7 de la mañana por una ladera hasta llegar a un templo a las 15 de la tarde. En la subida realiza numerosas paradas y su velocidad nunca es constante. Tres días después baja por el mismo camino empezando a la misma hora (7 de la mñn) y llega abajo a las 15 de la tarde. Lo hace de nuevo arritmicamente, a velocidad no constante y realizando alguna que otra parada.
La pregunta es:
¿¿¿Existe un punto en el que el monje esté a la misma hora en el mismo sitio en los dos días citados???
(ponle los puntos a Fidias da-beat, manke sólo sea 1)
Si uno piensa a los recorridos (o la altura en que se encuentra en determinado momento) como funciones continuas, la subida F:[7,15] —-> [0,h] y la bajada g:[7,15]—->[0,h] con f(7)=0 y f(15)=h, g(7)=h y g(15)=0 entonces la función f-g cumple que es continua y (f-g)(7)=-h y (f-g)(15)=h. Por Bolzano, existe un instante t en [7,15] tal que (f-g)(t)=0, es decir, tal que f(t)=g(t)
yo lo demostré así en su día Viasil, pero antes encontré una solución más visual k es imaginar un monje subiendo y otro bajando… obviamente se toparán en algún punto.
por cierto te toca poner un problema difícl.
Adew.
Cierto, 4053, fue Jordiel quien lo resolvió y a quien iba dirigida mi respuesta.
Ya he visto el nuevo problema difícil y la resolución. Lo de Bolzano se acepta, pero es demasiado complicado para las intenciones del blog. Por eso prefiero la respuesta de «imaginar que los dos días son el mismo» o «imaginar dos monjes el mismo día», es decir, superponer las dos trayectorias. Está claro que en algún momento se tienen que cruzar, es decir, están en el mismo sitio a la misma hora. Es uno de los enunciados del «Teorema del Punto Fijo».
Despues actualizo el post con los puntos, que ahora me voy a clase. Id pensando nuevos planteamientos, que los añado también.
Sí, es verdad que la solución de los dos monjes, uno subiendo y el otro bajando es más clara e intuitiva que la que yo dí, creo que no se me hubiera ocurrido pensarlo así (atrofia profesional 😦 )
Pero si se me la da por buena (a pesar de Bolzano:P), mando el problema DIFICIL (espero que no re-díficil):
16 personas deben resolver un problema en una serie de reuniones.
Para ello cada una las personas debe haber trabajado con las otras alguna vez, pero no pueden trabajar las 16 juntas. Cuando dos reuniones no tienen participantes en común se pueden realizar simultáneamente (es decir, el mismo día).
El objetivo es llevar a cabo el cometido en el menor número de días posibles.
Una posibilidad: el primer día podrían trabajar 15 personas juntas, y en los 15 días sucesivos cada una de estas 15 personas trabajar con la que quedo fuera el primer día. Se necesitarían entonces 16 días.
Otra posibilidad: se forman 2 grupos (A y B) de 8 personas cada uno: a1,…a8, el primero y b1,…,b8 el segundo. El primer día trabajan el grupo A y el B paralelamente. El segundo día a1 con b1, a2 con b2 hasta a8 con b8. El tercer día a1 con b2, a2 con b3 hasta a8 con b1. Se sigue así hasta el último día que se juntan a1 con b8, a2 con b1, a3 con b2 hasta a8 con b7. Se necesitan entonces 9 días.
1. ¿Es esta la cantidad de días óptima o se puede hacer en menos días?
2. ¿En cuántos y cómo?
Jeje, muy bueno lo de la atrofia profesional. Uno se acostumbra a hacer las cosas de la forma difícil (o fácil, según se mire) y se olvida de las fáciles (o más fáciles).
Me ha gustado tu nuevo planteamiento, ya lo he añadido al post, así como las puntuaciones. Siguen faltando planteamientos para los niveles fácil y medio. Fidias y Jordiel, creo que fueron los acertantes.
Hola da-beat,
mirá, releyendo el problema me di cuenta que falta agregar una cosa, sin la cual el problema no tiene mucho interés:
Dos personas que trabajaron juntas una vez ya no pueden volver a hacerlo.
(capaz se sobreentendió de las dos posibilidades dadas, pero hay que decirlo porque podría haber sido una trampa de los ejemplos, ¿no?)
Sin este dato es muy fácil ver que la tarea se podría hacer en dos días (usando el razinamiento de la primera posibilidad)
Lamento no haberlo puesto correctamente desde le principio 😦
Un saludo
silviq
Creo que te confundes da-beat,le toca a 4053 formular una de nivel medio.Si quieres pongo yo uno,pero no se me ocurre ninguno,sobre todo después de ver el último problema difícil.Con lo fácil que sería reunirse todos a la vez…
¿Os habeis enterado?¡Están saliendo en las noticias que están quemando todos los libros de matemáticas!¿Por qué?Porque dicen que tienen muchos problemas 😀
Viasil, ya iba a mandar la respuesta de los dos días pero me callé pensando que no había entendido el problema. Cierto que me toca el de nivel medio, pero esperad a que encuentre uno bueno.
4053 la verdad es que resolver los problemas no es lo complicado, resulta mas difícil tener que plantear uno después.
Pues nada al fácil que ya es hora.
NIVEL FÁCIL:
Un comerciante necesita hacer pesos desde 1kg hasta 500kg con incrementos de 1kg. Para ello decide comprar una balanza y las correspondientes pesas, pero para que le salga mas barato solo compra las pesas indispensables.
¿Cuantas pesas necesita como mínimo y cual será el peso de cada una?.
A ver, que me había liado con los planteamientos y las respuestas. Creo que ya me he puesto al día, y la situación está tal y como pone en el post principal, Hay planteamientos del Facil y Dificil sin resolver y el Medio está por plantear.
Las puntuaciones sí están correctas.
¡Ánimo a todos! Recordad que hay que llegar a 100 puntos, todavía no hay nada decidido.
¿Cuál es el siguiente número en la serie?
3, 7, 13, 21, 31, 43, 57, 73, 91, ???
Tal vez no es tan difícil pero una de series viene bien que hacía tiempo ya.
EN el difícil son sólo dos reuniones máximo por día?
Puesto que si creamos grupos irregulares en alguna reunión tendríamos algún trabajador parado, la forma que parece más optima seria crear grupos de personas divisores de 16.
2 grupos de 8, 4 de 4, u 8 de 2.
Con 2 grupos de 8 sería la segunda opción que nos da Viasil.
Con 4 grupos de 4 personas podríamos crear una sucesión parecida a la del ejemplo que nos daría 5 días, pero el último día dos se tendrían que repetir teniendo que desviar alguna persona a un sexto día.
Si los grupos son A, B, C y D, y para cada grupo numeramos A (a1, a2, a3, a4).
El primer día se reunirían los 4 del mismo grupo (por ejem. grupo A sería a1, a2, a3, a4. El segundo día los que tengan el mismo número de cada grupo (por ejemplo a1, b1, c1, d1). El tercer día (a1, b2, c3, d4). Y como a partir de este punto cualquier sucesión de 4 nos repetiría personas los hacemos de 3.
1º (a1, a2, a3, a4).
2º (a1, b1, c1, d1).
3º (a1, b2, c3, d4).
4º (a1, b3, c2).
5º (a1, b4, d3).
6º (a1, c4, d2).
Para el resto de grupos solo tendríamos que incrementar en uno su posición en el grupo, y del puesto 4 al 1
Para el caso de 8 grupos de 2 personas estaríamos en el mismo caso que la primera propuesta de Viasil salvo que el primer día solo se trabajaría también por parejas.
Solución más optima encontrada 6 días.
Ufff, he tardado en enviar y se ha metido 4053 por medio. Espero que no sean solo 2 reuniones xq toy con cara de asombro.
Ya que ha colgado el de nivel Medio y yo estoy conectado vamos a intentar resolverlo.
NIVEL MEDIO:
Solución: 111
3+4=7
7+6=13
13+8=21
….
73+18=91
91+20=111
De este me fio mas que del nivel difícil.
Fidias, tal vez sólo hay que afinar como se cuenta, pero ese es el camino.
Para el fácil (¡qué no es nada fácil!): (no estoy segura de que sea la solución)
se necesitarían 7 pesas, de pesos 1kg, 3 kg, 3^2=9 kg, 3^3 kg, 3^4 gk, 3^5 kg y 3^6 kg.
Para pesar 1kg tenemos la pesa. Para pesar 2 kilos, pondríamos la de tres en un platillo y la de uno en otro, pesando así dos kilos. Para 3 tenemos la pesa y para 4, ponemos juntas la de 3 y la de 1. De 5 a 13 hacemos lo mismo pero agregando la de 9.
si n <13, n=a*3^2+b*3+c (en base 3)
supomgamos que a=2, b=1, c=1 entonces escribimos n=3^3-3^2+3^2+3+1=3^3+3+1 (es decir, lo conseguimos con las pesas que tenemos).
si a=2, b=2, c=1 entonces n = 3^3-3^2+3^2-3+1 =3^3-3+1 (donde menos indica que lo pongo en el otro platillo, y lo conseguimos entonces con las pesas que tenemos).
Este razonamiento se puede hacer para cualquier número n y las distintas potencias de 3.
De 14 a 40, agregando 3^3 (40=3^3+3^2+3+1)
De 41 a 121 agragando 3^4
y así hasta llegar a 500.
Para conseguir sumar 500 necesitamos hasta la potencia 6 (de hecho, se podría pesar así hasta 1093 kg)
En el razonamiento anterior, donde dice n<13, debería decir n<27 y el razonamiento es para cuando agregué la pesa de 3^3
Para n<13
n=3^2+a*3+b
si a=2, b=1 , n= 3^2-3+1 (tengo todas las pesas)
si a=2, b=2 , n= 3^2-3+3-1= 3^2-1
Buneo, y todas las posibles combinaciones de a y b valiendo 0, 1, 2.
Se puede explicar mejor, lo sé ^_^
Bien Viasil, creo que la pata la metí yo. Se tendría que poder pesar hasta 1000kg y no hasta 500. (Recordé mal la cuestión.) Pero el señor comerciante queda igual de satisfecho en ambos casos 😉
Repasare el difícil, es bueno saber que he tomado el buen camino.
Bueno, al fin que tengo más de un segundo para entrar y al fin es viernes 🙂 .
Ya que Fidias dió por bueno el fácil, ahí va un nuevo problemita fácil:
con los números 1, 4, 5 y 6, usados todos una y sólo una vez, y combinados mediante las operaciones de suma, resta, multiplicación y división (las que se necesiten, las veces que hagan falta y no necesariamente todas), conseguir 24.
¡Qué lo disfruten! 🙂
Pues vaya con el fácil el rato que me ha costado, incluso después de haber comenzado por el camino lo descartaba. Pero al final salió.
5 / 4 = 1,25
1,25 –1 = 0,25
6 / 0,25 = 24
Espero que no exista otro camino, porque después de sacarlo seguí intentando encontrar otra forma.
Hay otra forma, pero es «casi» igual Fidias, no desesperes…
Capaz es más fácil intuirla si en lugar de trabajar con los decimales dejas la expresión escrita con fracciones 🙂
silviq
Es que me olvidé de decir algo importante: la solución de Fidias está perfecta, así que punto para Fidias 🙂
Sólo quería decir, que además de esa, hay otra solución, es que no tendría que escribir hasta poder hacerlo sin interrupciones 😦
no era facil, fidias merece 1.9 puntos.
saludos
Añadido el punto de Fidias pero, mientras propone uno nuevo, podéis seguir buscando la otra solución que propone Silvia (o silviq o Viasil 🙂 )
Ey! os toca poner problemas! toy’ ávido de enigmas… XD
adiew
Lo que me gustó del problemita de conseguir 24 es que uno descubre que cuesta romper con ciertos mecanismos de pensamiento. Al menos yo me resistí a las divisiones-fracciones porque no daban números enteros. Como preguntan mis alumnos: ¿esto está bien? es que me da 2/3… o_0
Y Fidias… te espera un montón de trabajo 🙂
Porque también acertó con el MEDIO, ¿no? (falta que le agregués los puntos da-beat). Así que, ya sabés, te toca proponer uno FÁCIL y uno MEDIO ¡y capaz también uno DIFÍCIL! 😉
tschüss
Si, Fidias había acertado también el medio. No le había puesto los puntos porque esperaba la confirmación de 4053, pero como no ha dicho que está equivocado, se da por bueno. Ya tiene los puntos añadidos, y pendientes dos planteamientos.
Saludos.
Cierto no lo dije pero como estaba bien explicado pensé k sobraba corroborarlo:
FIDIAS IS RIGHT.
debería haber problemas de calentamiento para cuando estamos en el banquillo, jejeje.
Salut!
Pues nada, recordando el problema de ViaSil para conseguir el número 24 yo os reto a uno parecido.
MEDIO:
Con los números 4, 5, 6 y utilizándolos una sola vez conseguir el 27.
FACIL:
Buscar un número primo compuesto por las cifras del 1 al 9 combinadas. Tienen que estar todas y no se pueden repetir.
Saludos.
Ya está actualizado el post. Nuevos problemas Fácil y Medio. Os recuerdo que el Difícil que planteó Viasil sigue esperando la solución… desde el 17 de Octubre.
Ánimo a todos.
Tengo una respuesta para el fácil. Creo que es imposible, porque los números de 1 a 9 suman 45, con lo que el número que formemos con esas cifras, con todas y sin repetir, será siempre múltiplo de 9. Y por tanto, no primo.
Sigo pensando el resto…
Un saludito.
4053, había un comentario tuyo que se lo había comido el mostruo del Akismet. Ya lo he restablecido. Perdónalo, a veces tiene hambre y come cosas que no debe.
Muy bien Fernando, te toca proponernos uno fácil que seguro que es una tarea más complicada que resolverlos
No me he olvidado de mis deberes, pero ando pensando en un problema fácil que, como bien dices, Fidias, es difícil de encontrar o plantear. Antes de que acabe esta semana lo pongo.
Vuelvo incumpliendo mis promesas, pero en fin… Disculpadme. Ahí va, en cualquier caso, el problemilla FÁCIL:
«¿De cuántas formas se pueden dsitribuir 44 monedas en 10 bolsillos, de manera que en cada bolsillo haya un número diferente de monedas?»
¡Un saludo!
Hola de nuevo!!! Si tiene hambre déjale k se coma algún comentario inoportuno da-beat. ya estoy de vuelta de tanto examen de ‘Diciembre’ hecho en Noviembre, veo que esto se ha movido poco así k estamos todos conel trabajo y/o exámenes.
Propongo la siguiente respuesta para el MEDIO aunque sé, o eso creo, k no es la respuesta k Fidias dará por válida:
RAIZ CUARTA[(4+5)^6]
saludos!!!
Fernando, creo que no se puede.
Si, por ejemplo, en el priimer bolsillo no ponés nada, no puede quedar entonces ningún otro bolsillo vacío.
Pero si en en el segundo bolsillo pongo una moneda y voy poniendo en los sucesivos bolsillos siempre un más que en el bolsillo anterior, necesitaría 1+2+3+…+9 monedas, y esto da 9*10/2=45.
besos para todos
silviq
Por cierto 4053, ¡acabás de abrir un mundo de soluciones! 🙂
Yo propongo
LA MITAD DE [(4+5)*6]
silviq
Jeje, creo que no vale ninguna. En la de 4053:
![\sqrt[4]{(4+5)^6}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B4%5D%7B%284%2B5%29%5E6%7D&bg=ffffff&fg=333333&s=0&c=20201002)
se utiliza el 4 dos veces y en la de Viasil:
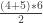
se utiliza el 2, que no debería estar.
Pero muy bueno el intento de escribirlo con letras 🙂
Gracias da-beat por corregir a 4053 y a Viasil. Hacia días que no me dejaba caer por aquí ya que había poco movimiento pero parece que ha arrancado la cosa otra vez. Seguiremos intentando el difícil de Viasil.
Un saludo
Creo que hablo por los dos si digo que ya lo sabíamos, pero si cuela pues cuela… jejeje.
Bueno, pues así es, Viasil. Has dado en el clavo. Era un simple problema de contar. ¿Te toca proponer el FÁCIL de resolver – DIFÍCIL de plantear.
Un saludito,
Fernando
Acá va un problema (pero no es de matemáticas 😦 )
En un reino muy lejano (no especifica si en el tiempo o el espacio, pero creo que no es importante) un rey decidió solventar una disputa entre dos caballeros de una manera, desde su punto de vista, muy ingeniosa e innovadora. Les propuso que hicieran una carrera de caballos y el ganador de la misma sería entonces quien tuviera razón. Pero lo ingenioso era que ganaría aquel cuyo caballo llegara último a la meta. Los caballeros montaron y …. no se movieron. Durante horas permanecieron inmóviles en sus briosos corceles. La contienda empezaba a ser un poco aburrida, con aspecto de poder llegar a durar varios meses, o años, o incluso, varias generaciones, cuando un sabio profesor de matemáticas, que estaba entre el público, se acercó a los jinetes, les susurró algo al oido y finalmente hubo un vencedor.
¿Qué fue lo que el sabio profesor de matemáticas dijo a los caballeros?
Pero bueno, si tiene que ser de matemáticas me pienso otro… 🙂
saludos
silviq
Se acepta, Viasil, no es necesario que sean de matemáticas, sino de pensar y razonar (eso son las matemáticas, ¿no?).
Actualizadas las puntuaciones y el nuevo problema Fácil.
Saludos.
Algo me dice k estoy desencaminado pero para el fácil propondría lo siguiente:
Unir a los caballos por una cuerda y que esta pase por un poste (árbol de aquel entonces) de manera que el caballo más fuerte obliga al más débil a llegar último.
Me parece una solución fea e impropia de un matemático así que seguiré buscando. XD
Salut!
O incluso (siempre con los caballos atados por la soga de antes) poner la meta entre ambos y los caballos tirando en direcciones contrarias… seguiré buscando.
4053, la primera propuesta de solución no la entiendo 😦 (en el contexto del problema)
La segunda no está mal (¡sos re recreativo!) aunque no es la respuesta al problema. Si bien no está dicho en forma completamente explícita, es una carrera «estándar», es decir, salen los dos de un punto y deben llegar a otro, corriendo en la misma dirección.
Pero dale, seguí mandando propuestas aunque suenen extravagantes 😉 , me encantan (como lo de la raíz cuarta 🙂 )
Un saludo
silviq
A mi también me ha gustado la segunda respuesta de 4053, es muy ingeniosa. Aunque no es la respuesta «esperada», bien podría valer.
Por cierto, parece que el problema Difícil va a necesitar de una pista. Ya ha pasado más de un mes y sigue sin resolverse. ¿O es que nadie lo está intentando?
Saludos.
Si matar a tu propio caballo no vale, habrá que buscar otra solución jeje.. Si ese reino no estuviese lejano en el tiempo, existirían las máquinas fotográficas. Si los jinetes hacen la carrera guiando a sus caballos hacia atrás (es decir, que avanzan de culo), y hacemos una foto justo cuando cruzan la línea de meta, cuando la enseñemos a cualquier persona/jurado/rey que no haya visto la carrera en directo y no sepa que corrían al revés, identificará como caballo ganador al que realmente perdió, así como identificaría al caballo perdedor como el ganador. De esa forma, el caballo que mas corre hacia atrás sería identificado como el último en llegar. Luego una posible solución al problema es hacer la carrera de culo y sin espectadores. La solución vendría del análisis de la foto finish :DD
Ya seeee, el punto flojo del argumento es que sería válido SOLO si NO ves la carrera en directo o la zona de meta NO está marcada la derecha o la izquierda de la línea de meta como zona de entrada (porque podrías distinguir cual de los dos llegó primero aunque fuese de culo), pero me ha hecho gracia mi propia ocurrencia estúpida 😛
Saludos!
Ahhh la mente busca la solución sola…
Ambos jinetes se cambian el caballo. Así, si por ejemplo el jinete A con el caballo de B llega primero a la meta, es el caballo de B el que ha llegado primero, y el de A después, ergo gana jinete A. ¿Por qué? Porque gana el jinete cuyo caballo llegue último a la meta. Al contrario igual…
El rey tenía su miga, porque supone que la habilidad del jinete en conducir al caballo es mas importante que la velocidad punta del caballo, cosa que no tiene por qué ser cierto. Pero claro, nadie a dicho que el rey fuese el el tio mas justo del mundo. Lo cierto es que era un cachondo…
Saludos!
Muy bien exiliado (digo, muy bien, exiliado 🙂 ), esa era al menos la respuesta que yo tenía al problema. El sabio dijo a los caballeros exactamente eso: intercambien los caballos.
Bueno, no sé a quién se le adjudicará la respuesta correcta. Podríamos hacer una carrera para dirimirlo, no? 😉
En todo caso, sea quien fuera, le toca lo díficil: poner el problema fácil.
Saludos
silviq
Sin duda esa respuesta tiene sentido… maldito sentido común, 3 cursos de mecánica cuántica y aún lo conservo! he caído de lleno en la trampa! ahhh!… no volverá a pasar.
Saludos.